Zvažte diskrétní distribuce. Jedna z podporovaných hodnot $ k $ $ x_1, x_2, \ ldots, x_k $ je určeno nezápornými pravděpodobnostmi $ p_1, p_2, \ ldots, p_k $ za podmínek, které (a) sčítají 1 a (b) koeficient šikmosti se rovná 0 (což odpovídá třetímu centrálnímu momentu, který je nulový). To ponechává $ k-2 $ stupně volnosti (ve smyslu řešení rovnic, nikoli statistického!). Můžeme doufat, že najdeme řešení, která jsou unimodální.

Abych usnadnil hledání příkladů, hledal jsem řešení podporovaná na malém symetrickém vektoru $ \ mathbf {x} = (- 3, -2, -1,0,1,2,3) $ s jedinečným režimem na $ 0 $ , nulový průměr a nulová šikmost. Jedním z takových řešení je $ (p_1, \ ldots, p_7) = (1396, 3286, 9586, 47386, 8781, 3930, 1235) / 75600 $ .

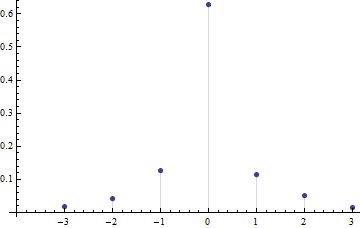
Vidíte, že je asymetrický.

Zde je zjevně asymetrické řešení s $ \ mathbf {x } = (-3, -1,0,1,2) $ (což je asymetrické) a $ p = (1,18, 72, 13, 4) / 108 $ :

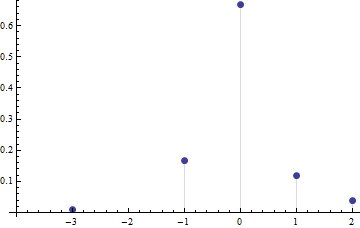
Nyní je zřejmé, o co jde: protože průměr se rovná $ 0 $ , záporné hodnoty přispívají $ 18 \ times (-1) ^ 3 = -18 $ do třetího okamžiku, zatímco kladné hodnoty přispívají $ 4 \ krát 2 ^ 3 = 32 $ a $ 13 \ krát 1 ^ 3 = 13 $ span >, přesně vyvážení negativních příspěvků. Můžeme použít symetrickou distribuci kolem $ 0 $ , například $ \ mathbf {x} = (- 1,0,1 ) $ s $ \ mathbf {p} = (1,4,1) / 6 $ a posunout trochu hmoty z $ + 1 $ do $ + 2 $ , malá hmotnost z $ + 1 $ až do $ - 1 $ a mírné množství hmoty až do $ - 3 $ span>, přičemž se ponechá průměr na $ 0 $ a šikmost na $ 0 $ , přičemž se vytvoří asymetrie . Stejný přístup bude fungovat k udržení nulové střední hodnoty a nulové šikmosti spojitého rozdělení při jeho asymetrii; pokud nejsme příliš agresivní s hromadným posunem, zůstane unimodální.

Upravit: Kontinuální distribuce

Protože se problém stále objevuje, dáme explicitní příklad s kontinuální distribucí. Peter Flom měl dobrý nápad: podívejte se na směsi normálů. Směs dvou normálů nebude fungovat: když zmizí její šikmost, bude symetrická. Dalším nejjednodušším případem je směs tří normálů.

Směsi tří normálů po vhodné volbě umístění a měřítka závisí na šesti skutečných parametrech, a proto by měla mít více než dostatečnou flexibilitu k vytvoření asymetrického řešení s nulovou šikmostí. Abychom nějaké našli, musíme vědět, jak vypočítat šikmost směsí normálů. Mezi nimi budeme hledat všechny, které jsou unimodální (je možné, že žádné nejsou).

Nyní obecně platí $ r ^ \ text {th } $ (necentrální) moment standardního normálního rozdělení je nula, když $ r $ je lichý a jinak se rovná $ 2 ^ {r / 2} \ Gamma \ left (\ frac {1-r} {2} \ right) / \ sqrt {\ pi} $ . Když změníme měřítko standardního normálního rozdělení tak, aby mělo standardní odchylku $ \ sigma $ , $ r ^ \ text {th } $ moment se vynásobí $ \ sigma ^ r $ . Když přesuneme jakoukoli distribuci o $ \ mu $ , nový $ r ^ \ text {th} $ moment lze vyjádřit pomocí momentů do $ r $ včetně. Moment směsi distribucí (tj. Jejich vážený průměr) je stejný vážený průměr jednotlivých momentů. Nakonec je šikmost nulová přesně, když je třetí centrální moment nulový, a to se snadno vypočítá z hlediska prvních tří momentů.

To nám dává algebraický útok na problém. Jedno řešení, které jsem našel, je stejná směs tří normálů s parametry $ (\ mu, \ sigma) $ rovnající se $ ( 0,1) $ , $ (1 / 2,1) $ a $ (0, \ sqrt {127/18}) \ přibližně (0, 2,65623) $ . Jeho průměr se rovná $ (0 + 1/2 + 0) / 3 = 1/6 $ . Tento obrázek zobrazuje pdf modře a pdf distribuce převrácené kolem své střední hodnoty červeně. Že se liší, ukazuje, že jsou oba asymetrické. (Režim je přibližně $ 0,0519216 $ , nerovná se průměru $ 1/6 $ .) Oba mají konstrukci nulovou šikmost .

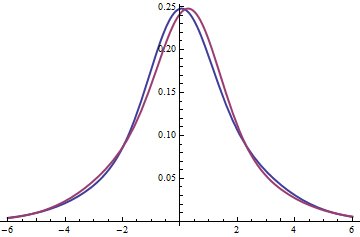
Grafy označují, že jsou unimodální. (Lokální maxima můžete zkontrolovat pomocí programu Calculus.)

Zde je jeden, který jsem našel na https://www.qualitydigest.com/inside/quality-insider-article/problems-skewness-and-kurtosis-part-one.html#, který jsem najít pěkné a reprodukované v R: inverzní Burr nebo Dagumovo rozdělení s parametry tvaru $ k = 0,0629 $ a $ c = 18,1484 $:

$$ g (x) = ckx ^ {- (c + 1)} [1 + x ^ {- c}] ^ {- (k + 1)} $$

Má průměr 0,5387, standardní odchylku 0,2907, šikmost 0,0000 a špičatost 2,0000. Zdroj jej také nazývá „distribuce slonů“:

Moje reprodukce v R byla vytvořena pomocí

  knihovna (pojistný matematik)
knihovna (knotR)

# nesymetrické rozdělení s nulovou šikmostí
# viz https://www.qualitydigest.com/inside/quality-insider-article/problems-skewness-and-kurtosis-part-one.html#

c < - 18.1484
k < - 0,0629

x <- seq (0,1,5, podle = 0,0001)

elephant.density <- dinvburr (x, k, c)
plot (x, elephant.density, type = "l")
polygon (c (min (x), x), c (min (elephant.density), elephant.density), col = "grey")
body (0,8,0,8, pch = 19, cex = 2)

# „uši“ vytvořené prostřednictvím https://www.desmos.com/calculator/cahqdxeshd
ear.x <- c (0,686; 0,501; 0,42; 0,68)
ear.y <- c (0,698; 0,315; 1,095; 0,983)

myseg (bezier (cbind (ear.x, ear.y)), type = "l")

EX <- gama (k + 1 / c) * gama (1-1 / c) / gama (k) # viz str. 6 https://wwz.unibas.ch/uploads/tx_x4epublication/23_07.pdf
EX2 < - gama (k + 2 / c) * gama (1-2 / c) / gama (k)
EX3 < - gama (k + 3 / c) * gama (1-3 / c) / gama (k)
(šikmost <- (EX3 - 3 * EX * (EX2-EX ^ 2) -EX ^ 3) / (EX2-EX ^ 2) ^ (3/2)) # nula až tři číslice: 0,0003756196
 

Jak ukazuje tento výstup, šikmost není u těchto hodnot parametrů zcela nulová až čtyřmístná. Zde je malý optimalizátor pro $ k $ a $ c $:

  # optimalizovat šikmost o něco dále
    skewval <- 1

while (skewval > 10 ^ (- 10)) {
  optskew.k <- uniroot (skewness.fun, lower = k * .95, upper = k * 1.1, tol = skewval ^ 2, c = c)
  skewval <- optskew.k $ f.root
  k <- optskew.k $ root
optskew.c <- uniroot (skewness.fun, lower = c * .95, upper = c * 1.1, tol = skewval ^ 2, k = k)
  skewval <- optskew.c $ f.root
  c <- optskew.c $ root
}
 

výtěžek

  tisk > (c)
[1] 18,89 306

> tisk (k)
[1] 0,05975542

> tisk (skewval)
[1] -1,131464e-15
 

Zvažte rozdělení na kladnou polovinu skutečné čáry, které se lineárně zvyšuje od 0 do režimu a poté je exponenciální vpravo od režimu, ale v režimu je spojité.

Dalo by se to nazvat trojúhelníkovo-exponenciálním rozdělením (i když často vypadá trochu jako žraločí ploutev).

Nechť $ \ theta $ je umístění režimu a $ \ lambda $ je parametr rychlosti exponenciálu.

S nárůstem $ \ lambda \ theta $ se distribuce postupně zmenšuje. Jak se $ \ lambda \ theta $ zvyšuje kolem $ \ přibližně 6,15 $, třetí okamžik přechází z pozitivního do negativního:

Brizzi (2006) $ ^ {[1]} $ označuje tuto rodinu distribucí jako distribuci „dvou tváří“ a pojednává o tomto bodě přechodu, kdy je třetí moment-skewness nula. von Hippel (2005) $ ^ {[2]} $ představuje příklad, který je téměř v tomto bodě přechodu zde

Vlákno Neobvyklé distribuce s nulovou šikmostí a nulovou nadměrnou špičatostí? obsahuje některé asymetrické příklady, včetně malého samostatného příkladu a dalšího spojitého unimodálního:

Diskrétní unimodální distribuce - nebo ekvivalentně vzorky - s nulovou šikmostí jsou poměrně snadno sestavitelné, velké nebo malé velikosti.

Zde je příklad, s nímž můžete zacházet jako se vzorkem nebo (vydělením hrubých frekvencí číslem 3000) jako pmf (hodnoty 'x' jsou hodnoty přijaté, znak 'n' je počet výskytů této hodnoty. ve vzorku):

  x: -2 -1 0 1 2 3 4 5 6 7 8 9 10
n: 496 498 562 1434 2 1 1 1 1 1 1 1 1
 

Tento příklad je sestaven z 3bodových distribucí:

  x: -2 1 c
n: c (c-1) (c + 1) / 6 c (c-1) (c + 1) / 3 - c 1
 

napříč různými hodnotami $ c $ mezi 3 a 10. Tento parametrizovaný (o $ c $) tříbodový „atom“ má $ \ sum_i n_ix_i = 0 $ a $ \ sum_i n_ix_i ^ 3 = 0 $, které v turn znamená, že směsi napříč různými možnostmi $ c $ mají nulovou šikmost. (Nemůžete udělat nic menšího než distribuce ve třech bodech, která má asymetrii a třetí centrální moment nula. Sbírka jednoduchých kousků pouze za několik bodů, jako jsou tyto, vytváří úhledné stavební bloky, ze kterých lze vytvářet větší struktury.)

Existuje mnoho různých dalších „atomů“, které lze vytvořit, ale tento příklad používá pouze tento jeden druh. K nějaké kombinaci atomů, jako jsou tyto, se přidává několik symetricky umístěných hodnot, které vyplňují zbývající díry a zaručují unimodalitu, aniž by došlo ke zničení struktury střední a třetí chvíle.

$ [1] $ Brizzi, M. (2006),
„Šikmý model kombinující trojúhelníkové a exponenciální rysy: Distribuce dvou tváří a její statistické vlastnosti "
Rakouský statistický věstník , 35: 4, p455–462
http://www.stat.tugraz.at/AJS/ausg064/

$ [2] $ von Hippel, P. T. (2005),
„Mean, Median a Skew: Oprava pravidla učebnice“
Journal of Statistics Education Svazek 13, číslo 2,
http://ww2.amstat.org/publications/jse/v13n2/vonhippel.html

Pro nulovou šikmost potřebujeme $$ \ operatorname {E} \ Big [\ big (\ tfrac {X- \ mu} {\ sigma} \ big) ^ {\! 3} \, \ Big] = 0 $$ nebo ekvivalentně $$ \ operatorname {E} \ Big [\ big (\ tfrac {X- \ mu} {\ sigma} \ big) ^ {\! 3} \, \ Big | X \ leq \ mu \ Big] + \ operatorname {E} \ Big [\ big (\ tfrac {X- \ mu} {\ sigma} \ big) ^ {\! 3} \, \ Big | X \ gt \ mu \ Big] = 0. $$

Nyní pro daný průměr a rozptyl vyberte libovolné dvě distribuce $ Y $ a $ Z $ s nulovou hmotností na pravé straně $ \ mu $ a $$ \ operatorname {E} \ Big [\ big (\ tfrac {Y- \ mu} {\ sigma} \ big) ^ {\! 3} \, \ Big] = \ operatorname {E} \ Big [ \ big (\ tfrac {Z- \ mu} {\ sigma} \ big) ^ {\! 3} \, \ Big] $$ a definovat $ X $ tak, aby odpovídalo $ Y $, pokud zbylo z $ \ mu $ a $ (\ mu - Z) $ jinak. (Neznáte přesnou notaci, kdokoli vám pomůže?)

Výsledná distribuce bude unimodální, pokud se PDF $ Y $ a $ Z $ zvětší nalevo od $ \ mu $ (kromě toho, že je nula napravo od $ \ mu $).

Následující diskrétní rozdělení je asymetrické a má nulovou šikmost: Prob (-4) = 1/3, Prob (1) = 1/2, Prob (5) = 1/6.Našel jsem to v příspěvku Doric et al., Qual Quant (2009) 43: 481-493;DOI 10.1007 / s11135-007-9128-9

Jistě. Zkuste toto:

  skew = function (x, na.rm = FALSE) {if (na.rm) x <- x [! Is.na (x)] #remove chybějící hodnoty součet ((x - průměr (x)) ^ 3) / (délka (x) * sd (x) ^ 3) #calculate skew} set.seed (12929883) x = c (rnorm (100, 1, .1), rnorm (100, 3.122, .1), rnorm (100,5, .1), rnorm (100, 4, .1), rnorm (100,1.1, .1)) zkosení (x) graf (hustota (x) )  

(Tvrdé věci jste již zvládli!)